The Gravitational Force of a 10 Solar Mass Black Hole vs a 10 Solar Mass Star: Understanding the Physics

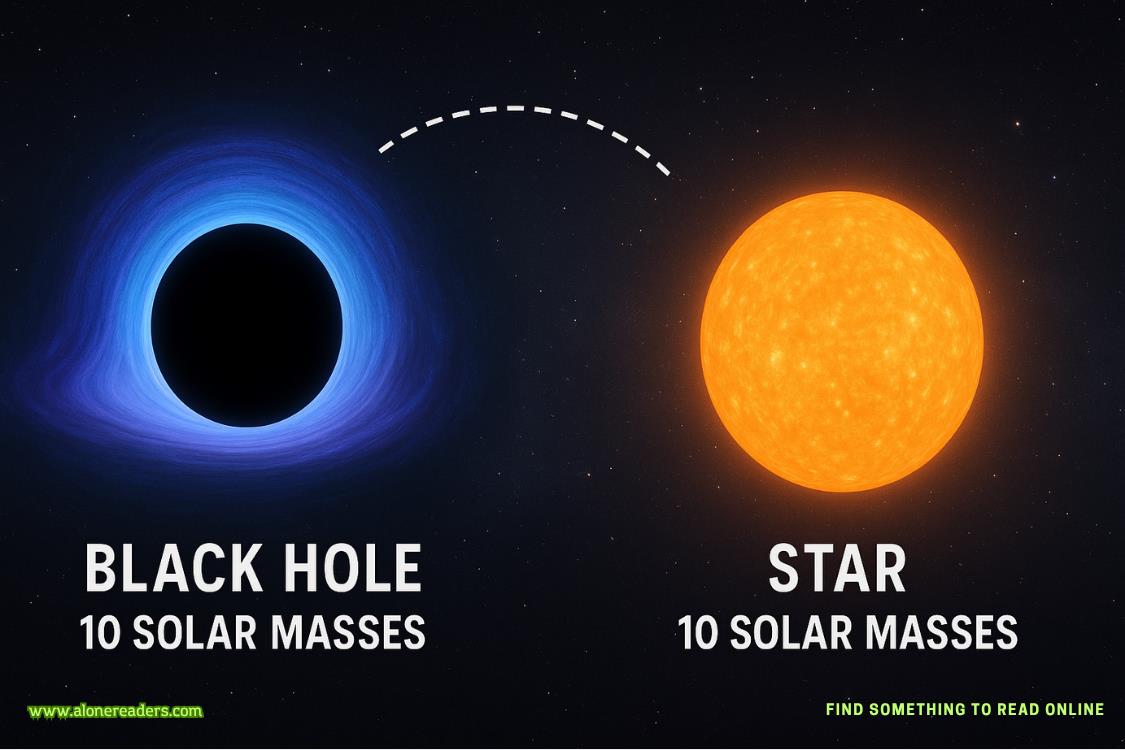
The universe is filled with extraordinary phenomena, and few are as mysterious or captivating as black holes. Among the most common questions that arise in the context of black holes concerns their gravitational force. Specifically, people often wonder: if a black hole has 10 times the mass of the Sun, does it exert more gravitational force than a star of the same mass? The short answer is that the gravitational force generated by a black hole with 10 solar masses is precisely equal to that of any other object—like a star—with 10 solar masses, as long as we consider objects at the same distance from the center of mass. Understanding why this is true requires a closer look at the fundamental physics of gravity and the distinctive nature of black holes.

Gravity is a universal force described by Isaac Newton's law of universal gravitation and, more comprehensively, by Albert Einstein's general theory of relativity. Newton’s law tells us that the gravitational force between two objects depends solely on their masses and the distance between their centers. The formula is:
F=G((m₁.m_2)/r²)
where FF is the gravitational force, GG is the gravitational constant, m1m1​ and m2m2​ are the masses of the two objects, and rr is the distance between their centers. Crucially, Newton’s formula makes no reference to what the objects are made of or their internal structure—it is the mass and the distance that matter.

This fundamental principle means that, from the outside, a black hole is just another massive object as far as gravity is concerned. If you were orbiting around a black hole with a mass of 10 Suns at a distance of, say, 30 million kilometers, you would feel exactly the same gravitational pull as you would if you were orbiting a regular star with the same mass at that same distance. The force does not depend on whether the mass is packed into a super-dense black hole or spread out as a luminous star. All that matters is the total mass and your distance from the center.

The confusion often arises because black holes are so exotic and their effects so extreme. A black hole is formed when a massive star exhausts its nuclear fuel and collapses under its own gravity. If the core is heavy enough—at least about three times the Sun’s mass—the collapse continues until the core becomes an infinitely dense point known as a singularity, surrounded by an event horizon. The event horizon is the "point of no return" beyond which nothing, not even light, can escape the black hole's gravity.

However, the key thing to remember is that the gravity a black hole exerts on objects outside its event horizon is governed by the same rules as any other object of equal mass. This is not just theory; it has practical implications. For example, if our Sun were replaced by a black hole of exactly the same mass, Earth’s orbit would not change—provided the black hole remained at the same distance. The planet would keep moving in its current path, feeling the same gravitational tug. Of course, the loss of sunlight would mean catastrophic consequences for life on Earth, but gravitationally, nothing would change.

This equivalence is a direct result of the equivalence principle in general relativity, which states that the gravitational field outside a spherical, non-rotating object (such as a star or a black hole) is determined solely by its total mass, regardless of what lies inside. General relativity further refines our understanding by describing gravity as the curvature of spacetime caused by mass and energy, rather than a force that acts at a distance. Still, for massive objects like stars and black holes, the external gravitational field is identical if the mass and distance are the same.

What, then, makes black holes seem so much more "powerful" than regular stars? The answer lies in their size. A star with 10 solar masses has a radius of millions of kilometers, emitting light and radiation from a vast, turbulent surface. In contrast, a 10-solar-mass black hole compresses all its mass into a region just a few tens of kilometers across—its event horizon. This extreme compactness creates an enormously steep gravitational gradient near the black hole, so that if you venture close enough, the force of gravity increases dramatically in a very short distance. This leads to the famous "spaghettification" effect, where the difference in gravity between your head and feet would stretch you apart if you fell toward a stellar-mass black hole.

But again, at any distance greater than the event horizon, and particularly at astronomical distances, the gravity you experience is the same as it would be for a regular star with the same mass. For example, stars in a binary system orbiting a black hole respond only to its total mass, not its exotic nature. The orbits are governed by the same laws that describe planets circling stars. This is why astronomers can detect black holes by observing the motion of stars in binary systems: a star orbiting an invisible but massive object behaves just as if it were orbiting a massive star, until you realize no light is coming from its companion.

Black holes do have unique effects that stars do not, such as the ability to warp spacetime enough to produce gravitational lensing, or to accrete and heat matter to produce powerful X-rays and jets. These effects arise from the black hole's compactness and the extreme gravitational fields near the event horizon, not from an increase in the overall gravitational pull at a distance.

A common misconception is that black holes act as cosmic vacuum cleaners, sucking in everything around them with irresistible force. In reality, black holes do not attract matter any more strongly than a star of the same mass. Objects must still lose enough energy to cross the event horizon. Matter can orbit black holes just as it orbits stars, unless it comes close enough to be drawn inside. In fact, in many galaxies—including our own—the supermassive black holes at their centers sit quietly, surrounded by stars and gas that orbit them without plunging in.

The reason black holes seem so dramatic is that they concentrate an enormous mass into a very small space, creating an extreme environment close to the event horizon. If you replace the Sun with a black hole of equal mass, the event horizon would have a radius of only about 3 kilometers, compared to the Sun's radius of about 700,000 kilometers. At this close range, the gravity would become incredibly strong, but at Earth's distance, it would be no different than the gravity of the Sun.

This understanding is central to the study of astrophysics and the behavior of objects in the universe. It also allows astronomers to study the motion of stars, gas clouds, and even light to infer the presence and mass of black holes. These observations are how we know that many stellar-mass black holes exist, and how we have measured the mass of the supermassive black hole at the center of our galaxy.

To summarize, the gravitational force generated by a black hole 10 times the mass of the Sun is exactly the same as that of a star with 10 solar masses, as long as we compare them at the same distance. This is a direct consequence of the laws of gravity, which care only about total mass and distance—not the form that mass takes. What sets black holes apart is not their total gravitational pull at a distance, but their incredibly compact size, which creates extreme environments near the event horizon. This knowledge not only dispels common myths about black holes, but also underscores the elegance and predictability of the laws that govern our universe.